COMPILADORES - DISEÑO Y CONSTRUCCION

Un compilador es un programa traductor que lee un programa en código fuente y genera un programa en codigo objeto, tambien puede dar como resultado los erróres de diagnóstico, en tal caso no se genera programa objeto. para conocer mas acerca de este tema puede seguir el siguiente link donde encontrará un documento referente a este tema.

PARCIAL DE TEORIA DE GRAFOS

ALGORITMO DE PRIM
EJERCICIO SOBRE ARBOL GENERADOR MINIMO
Use el algoritmo de PRIM o de KRUSKAL para encontrar el árbol generador mínimo del siguiente grafo valorado

VEA LA SOLUCION AQUI

VERTICES FUENTE Y SIFON

VERTICE FUENTE: Se dice que un vertice es fuente en un digrafo cuando de el solo salen aristas y no llegan.
VERTICE SUMIDERO O SIFON: Es el vertice de un digrafo donde unicamente llegan aristas y no sale ninguna de el.
ejemplo:

GRAFO ISOMORFO

Dos grafos son isomorfos si se puede transformar uno en el otro simplemente renombrando los vértices.

GRAFO BIPARTITO

Un Grafo bipartito se denomina en Teoría de grafos a un grafo cuyos vértices se pueden separar en dos conjuntos disjuntos V₁ y V₂ y las aristas siempre unen vértices de un conjunto con vértices de otro:

• 
• 
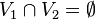
• no existe ninguna arista e = (x₁,x₂) ni e = (y₁,y₂)

Grafo bipartito completo K_2,3

Siendo V el conjunto que contiene todos los vértices del grafo.

El conjunto de todos los grafos bipartitos es denominado ; en particular, un grafo bipartito uniendo dos conjuntos, de m y n elementos, respectivamente, se denota por , o, simplemente, K_m,n.

Un grafo bipartito en el cual todos los elementos de V₁ están unidos con todos los elementos de V₂ se denomina bipartito completo

Los grafos bipartitos suelen representarse gráficamente con dos columnas (o filas) de vértices y las aristas uniendo vértices de columnas (o filas) diferentes.

Un árbol.

Un grafo sin ciclos de tamaño impar.

PUENTES DE KöNIGSBERG

El problema de los siete puentes de Königsberg (Prusia oriental en el siglo XVIII -ciudad natal de Kant- y actualmente, Kaliningrado, en la óblast rusa de Kaliningrado) es un célebre problema matemático que fue resuelto por Leonhard Euler en 1736 y dio origen a la Teoría de los grafos.

Consiste en lo siguiente:

Dos islas en el río Pregel que cruza Königsberg se unen entre ellas y con la tierra firme mediante siete puentes. ¿Es posible dar un paseo empezando por una cualquiera de las cuatro partes de tierra firme, cruzando cada puente una sola vez y volviendo al punto de partida?

Euler enfocó el problema representando cada parte de tierra por un punto y cada puente, por una línea, uniendo los puntos que se corresponden. Entonces, el problema anterior se puede trasladar a la siguiente pregunta: ¿se puede recorrer el dibujo terminando en el punto de partida sin repetir las líneas?

Euler demostró que no era posible puesto que el número de líneas que inciden en cada punto no es par (condición necesaria para entrar y salir de cada punto regresando al punto de partida por caminos distintos en todo momento). En teoría de los grafos esta idea se corresponde con la posibilidad de encontrar un Ciclo Euleriano en un grafo.